Sketch2Go - fördert die visuelle Erforschung von Phänomenen durch die qualitative Angabe der Art und Weise, wie sich die vom Benutzer gezeichnete Skizze ändert. Die Skizze ist eine schematische Darstellung, die versucht, den Betrachter auf die Prinzipien und nicht auf langwierige Details des dargestellten Phänomens zu konzentrieren. Das Phänomen kann sich auf Prozesse außerhalb der Mathematik beziehen (z. B. physikalische zeitliche Phänomene) oder auf mathematische Phänomene (z. B. eine Funktion mit drei Extremen). Das Bewegen von Schülern über die Plot- und Lesepunkte hinaus, um die globale Bedeutung von Graphen zu interpretieren und die funktionalen Beziehungen, die sie beschreiben, wurde als ein Hauptziel der Mathematikausbildung identifiziert.
Werkzeuge wie Sketch2Go ermöglichen die Umgehung von algebraischen Symbolen als einzigen Kanal in die mathematische Darstellung und motivieren die Schüler, mit einer gegebenen Situation zu experimentieren, sie zu analysieren und zu reflektieren, auch wenn die Situation zu kompliziert ist, damit sie symbolisch anlaufen. Die visuelle Analyse, die sich aus der Arbeit mit solchen Werkzeugen ergibt, unterscheidet sich von derjenigen, die aus der Arbeit mit algebraischen Symbolen oder numerischen Tabellen entsteht.
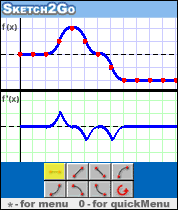
Eigenschaften Sketch2Go ist ein qualitatives Grafik-Tool. Die Diagramme werden unter Verwendung von sieben Symbolen skizziert, die konstante, zunehmende und abnehmende Funktionen repräsentieren, die sich mit konstanten, ansteigenden oder abnehmenden Raten ändern. Es basiert auf der ursprünglichen R & amp; D, die von Schwartz und Yerushalmy (1995) und Shternberg & amp; Yerushalmy (2001), die auf der Grundlage der Funktion und ihres Vokabulars eine Zwischenbrückendarstellung vorschlagen. Die sieben grafischen Symbole beschreiben die Veränderung sowohl der Funktion als auch ihrer Änderungsrate. Sketch2Go ist eine Version des Qualitative Derivative Grapher, die von Alexander Zilber für CET (Center for Educational Technology) programmiert wurde.
Mathematische Modellierung kann nicht vollständig durch dieses qualitative Zeichen-System von konstanten, zunehmenden und abnehmenden Funktionen erreicht werden. Aber der Satz von sieben Zeichen unterstützt die Bildung einer mathematischen Konstruktion mit der Sprache entwickelt aus der Bekanntschaft mit physikalischen Szenarien, helfen, legen die Grundlagen des Lernens Pre-Kalkül und Kalkül. Sketch2Go unterstützt die Abstraktion von alltäglichen Phänomenen mit einem kleinen Satz mathematischer Zeichen, die auf dem Bildschirm als halbbetonte Objekte manipuliert werden können.
Vorgeschlagene Aktivitäten
Ein ModellierungsproblemEin Auto bewegt sich mit einer Geschwindigkeit von 20 Metern pro Sekunde, wenn der Fahrer sieht, dass ein Ball auf der Straße rollt. Die Reaktionszeit des Fahrers beträgt eine Sekunde (Reaktionszeit ist die Zeit, die zwischen dem Erkennen der Kugel und dem Drücken der Bremsen vergeht). Während dieser Zeit fährt das Auto mit seiner konstanten Geschwindigkeit fort. Nachdem der Fahrer die Bremsen betätigt hat, bremst das Fahrzeug für 7 Sekunden, bis es anhält.
* Beschreiben Sie in einem Diagramm die Entfernung, die das Auto von der Zeit, als der Fahrer den Ball sah, bis zum Stillstand des Fahrzeugs zurückgelegt hat.
* Was beschreibt der untere Graph in dieser Geschichte?
* Wie würde sich Ihr Graph in jeder der folgenden Situationen ändern: (1) der Fahrer fuhr schneller; (2) der Fahrer war betrunken; (3) es war ein regnerischer Tag.
Verwenden von Skizzen zur Ableitung von Ableitungsregeln
Skizzieren Sie Beispiele für Funktionen, die die unten aufgeführten Bedingungen erfüllen würden.
Schreiben Sie die Eigenschaften, die die Funktionen repräsentieren oder argumentieren, warum Sie solche Funktionen nicht finden konnten:
* Kontinuierliche Funktionen deren Ableitungen monoton zunehmen
* Ununterbrochene Funktionen, die abgeleitete Funktionen mit genau einem einzelnen Maximum haben* Kontinuierliche Funktionen mit abgeleiteten Funktionen, die eine Diskontinuität oder eine Art haben
* Funktionen mit Diskontinuität, die kontinuierliche Ableitungen haben
* Funktionen, die stetige Ableitungen und eine zweite Ableitung mit Diskontinuität haben
Was ist neu in dieser Version:
& Middot; Zeichnung speichern
& Middot; Posteingang
& Middot; Einstellungen
& Middot; Verbesserte Grafik
& Middot; Fehlerbehebung
Einzelheiten der Anwendung:
Version: 0.84
Upload-Datum: 28 Apr 11
Entwickler: Math4Mobile
Lizenz: Frei
Popularität: 158
Größe: 97 Kb



Kommentare nicht gefunden